EMAS in multi-criteria optimisation
When a lot of different (often contradictory) factors have to be considered, the decision-maker deals with an ambiguous situation: alternatives that are optimal from the point of view of one criterion may turn out to be absolutely unacceptable considering the others. This situation is reflected by the notion of *Pareto optimality*.
A variety of evolutionary multi-criteria optimisation techniques have been proposed. The elitist and non-elitist algorithms were distinguished by the typology of evolutionary multi-objective algorithms (EMOAs). The main difference between these two groups of techniques consists in utilizing the so-called elite-preserving operators that give the best individuals (the elite of the population) an opportunity to be directly carried over to the next generation, regardless of the actual selection mechanism used. Of course, if the algorithm finds a better solution than the one in the elite, this solution becomes a new elitist solution. Unfortunately, in the case of multi-criteria optimisation, since there are multiple objective functions, it is not as straightforward as in the single-objective case to identify the elite. In such situations, the non-dominating ranking comes to our rescue.
During research to date, many different realisations of EMAS-based multi-objective optimisation problems solvers have been proposed, e.g. elitist multi-objective EMAS, EMAS with cultural and immunological mechanisms and the whole set of coevolutionary EMASs. In the next Section, elitist evolutionary multi-agent system (elEMAS) will be briefly described as a good illustration of multi-objective EMAS.
Elitist evolutionary multi agent system for multi-objective optimisation
Elitism can be introduced into EMAS in many different ways. In the case that is considered, it is based on a slightly modified structure of environment (see figure below). Compared to the structure of environment shown in section that treats of EMAS, modifications consist in introducing an additional, the so-called elitist island and special actions that can be performed (only) by selected agents, allowing them to migrate to this very island. The elitist island only accepts immigrant agents, there is no outbound migration from there. Thus agents which have decided to migrate to this island are not able to go back from elitist to ordinary island(s), and cannot take part in the process of evolution.
A mechanism allowing to identify elitist agents is based on the level of additional resource called prestige (shown as a size of trophy in figure below), which is gathered (and is not lost) by agents during their life. At the beginning of their life, the level of prestige equals zero. Then, every time an agent dominates (in a sense of domination relation) any other agent, its level of prestige increases, and so it may be assumed that agents with a high level of this specific resource belong to the elite. This mechanism allows the realisation of the above-mentioned idea of non-dominating ranking in a really elegant, easy to understand and implement way that does not require any additional complicated operations and computations.
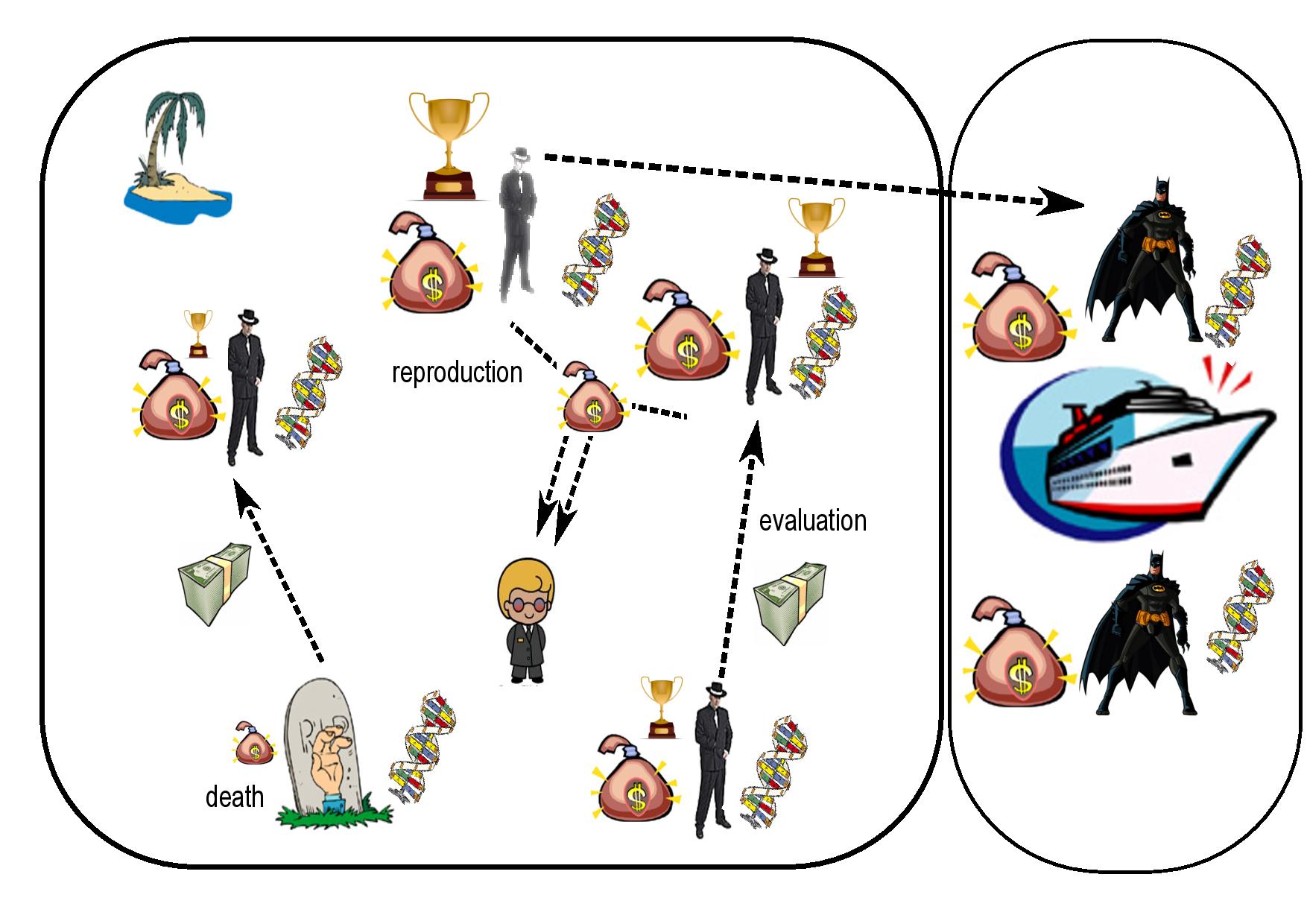
It turns out that applying elitist operator(s) to an evolutionary multi-agent system – despite other presented advantages – gives an opportunity to introduce additional mechanism(s) responsible for improving the spreading of the individuals over the Pareto frontier. One of such mechanisms can be realized as follows: during meetings, an agent is able to check if a solution represented by its opponent is located in its surroundings at the frontier (i.e. if the distance between solutions represented by agents is less than a given value ε). If so, the agent increases its personal counter storing the number of individuals located in the same fragment of the Pareto frontier. Additionally, asking its opponents about the number of individuals located in their surroundings, the agent is able to gather with time (partial) knowledge of the average number of individuals located in some areas of the Pareto frontier (i.e. in surrounding areas represented by agents it met). Consequently, if the agent becomes the elitist one, it can make a decision about migrating to the elitist island only when the number of individuals located in its surroundings is greater than the average number of individuals located in other regions of the Pareto frontier.
The mechanism described allows deeper exploration of those areas of the Pareto frontier which are worse sampled than its other regions. A similar mechanism can also be applied to the space of decision variables, thus concerning the Pareto set. Of course both mechanisms can be used simultaneously, and this can be of great importance in real-life problems where both, Pareto set and Pareto frontier are often disconnected.
Additionally, ε parameter can be managed adaptively by agents. In the simplest form, it can be linearly smaller and smaller with the agent’s lifetime. In more advanced implementations it can be decreased by agents on the basis of their interactions with the environment and other agents.
Multi-criteria optimisation in noisy environment
Considering advantages of EMAS-based optimisation solvers over classical evolutionary algorithms, the so-called soft selection has to be underlined. Unlike classical algorithms, if an individual is dominated by another one, it is not immediately removed from the population but its energy level is decreased (depending on parameter values) so it has to be dominated several times to be eventually removed from the population.
Such a mechanism can be especially important if optimisation in a noisy environment is considered. Unlike mathematical models, in real-life problems noise cannot be avoided and it may come from many different sources, e.g. distortions in input data, wrong sampling, as well as approximation faults. In such an environment, worse solutions may be falsely perceived by the algorithm as better ones. Consequently, worse solutions may be carried over to the next generations. It depends of course on the ‘scale of noise’ but it is possible that in this case the algorithm will drift towards the misleading ‘optimal’ result set.
